Bílý a šedý pěnový polystyren a princip jeho tepelně izolační funkce

Pod názvem NEOPOR – tepelná izolace nové generace [1] byl v září 2005 uveřejněn článek, který přinesl fyzikální popis tepelně izolačního chování bílého a šedého pěnového polystyrenu. Čtenář internetové verze tohoto časopisu L. K. si ve vzorci pro výpočet radiační složky šíření tepla všiml nepříjemné chyby. Panu L.K. velmi děkujeme za upozornění. V tomto příspěvku přineseme opravu a podrobnější výklad podstatných předpokladů a důsledků této teorie "polystyrenu“.

Pro úplnost ocitujme reakce pana L. K. tak, jak došly od čtenáře na internetový portál http://www.stavebnictvi3000.cz. Reakce se týkaly nesouladu vzorců, zejména vzorce (6), s prezentovanými výsledky.

Datum: 18.12.2006, 01:07 Autor: Leoš Klofáč
Nadpis: vztah (6)

Tady je vztah (6), jak jej vyplivl Matlab integraci vztahu (5). Víc zjednodušit se mi to už nepodařilo.

Použitím tohoto vzorce se dojde ke stejným závěrům, jaké jsou uvedeny v článku.

Po upozornění čtenáře jsme vzorec (6) podrobili kontrole. Pan Leoš Klofáč má pravdu, chybou autora předmětného článku byl otištěn chybný vzorec, který neodpovídal integraci rovnice (5) v článku [1]. Ač se zprvu zdálo, že také interpretace integrálu (6) v bodech A) až E) bude chybná, zjistili jsme (podobně jako později i pan Klofáč), že interpretace odpovídá správné integraci rovnice (5). Abychom nepříjemnou chybu alespoň v rámci možností napravili, zvolili jsme pro snazší a přehlednější výpočet integrálu strukturovanější postup a názornější substituce. Další změnou byla volba r = 0 v součinu fotometrických parametrů k·(1-r) ve vzorci (5). K důvodům tohoto kroku se ještě vrátíme. Vzorec (6) po správné integraci (5) má pak tento tvar

   (6)

kde σ = 5,67·10^-8 W·K^-4·m^-2 je Stefanova - Boltzmannova konstanta,
       T_int a T_ext jsou termodynamické teploty teplejší resp. chladnější plochy izolantu,
       k (m^-1) je součinitel absorpce,
       L je tloušťka deskového izolantu a
       A a B je bezrozměrná „dolní” (teplá) resp. „horní” (studená) integrační konstanta. Obě jsou dané předpisem

   resp.

   

Rozbor důsledků

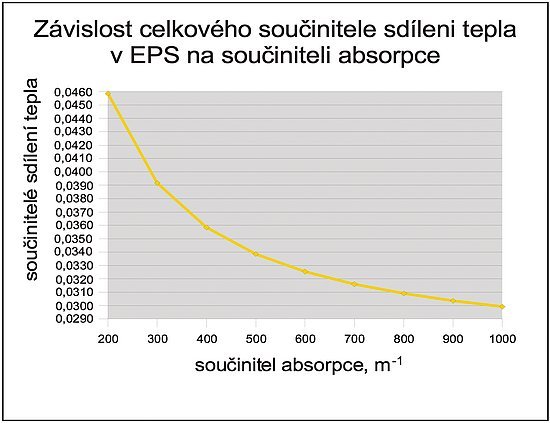
Obr. 1: Závislost velikosti sdílení tepla sáláním v pěnovém polystyrenu na velikosti absorpčního součinitele (červená křivka). Uhlíkaté úpravy se používají pro zvýšení součinitele absorpce cca od 100 m^-1 výše. Žlutá křivka znázorňuje celkový součinitel sdílení tepla, v němž je zahrnut příspěvek vodivosti. V hodnotě součinitele tepelné vodivosti tak, jak vycházi z makroskopických měření, je vždy významný podíl sálavé složky výměny tepla.

Jak vlastně interpretovat výsledek daný rovnicí (6), která je ekvivalentní se zápisem pana L.K. Na obr. 1 je graf, který ukazuje závislost celkového součinitele sdílení tepla v expandovaném pěnovém polystyrénu (EPS) a součinitele sdílení tepla sáláním (radiací) v témže materiálu na součiniteli absorpce. Celkový součinitel sdílení tepla (žlutá křivka) je součtem součinitele tepelné vodivosti λ a součinitele sdílení tepla radiací λ_s (červená křivka). Připomeňme, že součinitel tepelné vodivosti je zde postaven λ = 0,026 W·m^-1·K^-1 (hodnota pro vzduch) a součinitele sdílení tepla sáláním se pak určí podle vzorce

kde I_s je hodnota z (6) a
      d je tloušťka izolantu.

Obr. 2: Závislost celkového součinitele sdílení tepla (součinitele tepelné vodivosti) na velikosti absorpčního součinitele.

Z opravené rovnice (6) plyne, že úpravy uhlíkatým práškem nanometrových rozměrů v šedém pěnovém polystyrénu (NeoFloor, GreyWall, NEOPOR) se projeví ve zvýšení absorpčního součinitele z cca 370 m^-1 (bílý EPS o hustotě 15 kg/m³) na dvojnásobek. Tím klesne součinitel tepelné vodivosti z hodnoty 0,037 W/(mK) na 0,032 W/(mK). Stejného efektu pak docílíme (podle Lambertova - Beerova¹ zákona a z praktické zkušenosti) zdvojnásobením objemové hmotnosti pěnového polystyrénu. Tato tvrzení znázorňují také grafy na obr. 1 a obr. 2, které jsou grafickým vyjádřením opraveného vztahu (6). Je třeba upozornit na citlivost, s jakou reaguje celková tepelná vodivost materiálu na zvýšení součinitele absorpce: Zvýšení z k = 400 m^-1 na k = 500 m^-1 představuje podle grafu na obr. 2 pokles součinitele tepelné vodivosti λ o 0,002 Wm^-1K^-1. Zvýšení z k = 800 m^-1 na k = 900 m^-1 už jen o 0,0005 Wm^-1K^-1. Z toho je vidět, že chyba v odhadu součinitele vodivosti vzduchu v řádu 10 % nebo zanedbání vlastní vodivosti polystyrénu v pěnovém materiálu může velikosti součinitele absorpce, které tato teorie předpovídá, posunout na polovinu nebo naopak na dvojnásobek.

Další důsledky uvedené v bodech A) až D) původního článku [1] zůstávají i po opravě vztahu (6) v platnosti. Také tvrzení E) je v souladu s opraveným vztahem (6), pokud v rovnici (5) v původním textu [1] postavíme r = 0 a k = 736.

Zastavme se nyní u fyzikální podstaty celé teorie, jejímž prubířským kamenem je výsledek přímého měření součinitele k pro tepelné záření odpovídající teplotě kolem 13,5 °C (střed mezi okrajovými teplotami 21 °C a –15 °C) a tedy s maximální spektrální hustotou pro vlnovou délku 10 μm. Měření by mělo ukázat, že pro bílý EPS o objemové hmotnosti 15 kg/m³ je k ≈ 400 m^-1. Přesné přímé měření absorpčního součinitele by zejména umožnilo lepší parametrické nastavení teorie, která je v tomto případě aplikována na pěnový polystyrén.

Co se týče korektnosti vlastní teorie, ke které se vztahují některé čtenářské dotazy, jejím základem je Lambertův - Beerův zákon pojatý „na ruby”. Tento zákon, který má v diferenciálním zápisu tvar

dI = – k.I.dx

počítá změnu intenzity záření po průchodu nekonečně tenkou vrstvou materiálu. Pokles intenzity prošlého záření je úměrný pohltivosti (absorbanci) vrstvy α, která se u této vrstvy rovná k·dx. V našich úvahách však tato nekonečně tenká vrstva vystupuje také jako plošný zářič tepelného záření o intenzitě

dI = σ.T⁴.k.dx

Tento diferenciální vzorec je Stefanův Boltzmannův zákon použitý na nekonečně tenkou vrstvu tloušťky dx o termodynamické teplotě T, jejíž emisivita (sálavost) ε je rovna σ·k·dx a relativní emisivita k·dx. Rovnost relativní emisivity ε a pohltivosti α je pak v souladu s posledním povinným předpokladem (Kirchhoffův zákon), který říká, že aby měl tepelný zářič v ustálených podmínkách konstantní teplotu, musí stejnou energii vyzařovat a zároveň pohlcovat, tzn. že relativní emisivita zářiče je rovna pohltivosti zářiče.

Záření, které naše zkoumaná, infinitezimálně tenká vrstva izolace dx, umístěná ve vzdálenosti x (0 ≤ x ≤ L) od teplého okraje izolace sálá, prochází skrze zbylou izolaci tloušťky L–x ke studenému okraji izolace. Na této cestě se oslabí (podle integrálního Lambertova - Beerova zákona) na velikost

dI₊ = σ.T⁴.k.dx.e^-k(L-x)

a je pohlceno materiálem na studeném okraji, o němž se předpokládá, že je dokonale pohltivý. Může jím být třeba hustá tenkovrstvá omítka tloušťky 5 mm, kterou záření o délce vlny 10 μm neprojde, ani se od ní neodráží.

Studený okraj také vyzařuje teplo a část z něho vrací naší zkoumané vrstvě izolace tloušťky dx. Protože považujeme studený povrch za dokonale pohltivý, intenzita jeho vyzařování je σ.T⁴_ext. Po projití skrze izolaci tloušťky L–x ke studenému okraji dorazí ke zkoumané vrstvě dx izolace tok záření o intenzitě σ.T⁴_ext. e^-k(L-x) a vrstva z něho pohltí část vyjádřenou násobkem dopadající intenzity a pohltivosti zkoumané vrstvy α = k·dx, tedy celkem

I_- = σ.T⁴_ext.e^-k(L-x).k.dx

Rozdíl I = I₊ – I₋ představuje celkovou výměnu zářivé energie mezi zkoumanou vrstvou dx a studeným okrajem. Pokud provedeme součet výměny zářivé energie mezi všemi vrstvami izolantu a studeným okrajem a k němu připočteme výměnu tepla mezi teplým a studeným okrajem, dostaneme vzorec pro velikost transportu tepla zářením mezi teplým okrajem a izolantem na jedné straně a studeným okrajem na druhé straně

   (5)

To je vzorec (5) v původním článku, ovšem pro odrazivost r = 0. Pro k = 0 je integrál (5) nulový, což odpovídá tepelnému sdílení mezi teplým a studeným okrajem v mezeře bez izolace. Pro k = ∞ je sdílení tepla zářením nulové, což je případ pevných hutných látek, kde se transport tepla děje vedením. Důvod pro volbu odrazivosti r = 0 pro bílý i šedý polystyren (na rozdíl od původního článku [1]) je tento:

Tepelné záření o délce vlny 10 μm nemůže ve struktuře mnohem tenčích mezibuněčných stěn expandovaného polystyrénu a také na uhlíkových částicích nanometrových rozměrů u šedého polystyrénu (NeoFloor, GreyWall, NEOPOR) vykazovat klasický „fresnelovský” tzn. pružný odraz. Jak tenká stěna, tak uhlíkatá absorpční částice v expandovaném polystyrenu může tepelné záření (kvantum) pouze pohltit, následně zvýšit svou vnitřní energii a po chvíli (a na jiném místě) jiné kvantum záření zase uvolnit, tím snížit teplotu a vnitřní energii atd. Pohlcené a později vyzářené elektromagnetické kvantum nelze tudíž považovat „jen” za odražený původní paprsek. Záření, které není v daném místě izolantu pohlceno, se neodráží, ale prochází izolantem hlouběji a může být pohlceno jinde.

Přibližme postup řešení integrálního členu v rovnici (5). Lze jej rozložit na dva integrály, z nichž ten, kde vystupuje čtvrtá mocnina T_ext je triviální. Zbývající člen

   (5.1)

spočítáme např. takto: Položíme

a zavedeme substituci

Integrál (5.1) pak dostane tvar

Integrací posledního výrazu (primitivní funkci k integrandu spočítáme postupem per partes nebo najdeme v tabulkách neurčitých integrálů) stanovíme integrál (5.1). Integrací zbylých členů rovnice (5) pak dostaneme vztah (6), jak bylo dokázati.

Ačkoliv je nyní čtenářům předloženo správné řešení rovnice (5), která je matematickou formulací jednoduché a tudíž věrohodně vypadající fyzikální úvahy založené na známých fyzikálních zákonech (Lambertův a Berrův zákon a dále Kirchhoffův zákon, který vyjadřuje zákon zachování energie, resp. princip kontinuity toku zářivé tepelné energie na lokální úrovni), jedna otázka stále zůstává. Totiž jestli platí klíčový předpoklad, který ovšem nemá oporu v žádném zákoně, že v pěnovém materiálu v ustálených teplotních podmínkách klesá teplota lineárně se vzdáleností od teplého okraje ke studenému. Ve stavební praxi se tato linearita bere automaticky.

Také na makroskopické úrovni však musí vždy platit, že celkový tok energie, realizovaný společně vedením a sáláním tepla mezi teplým a studeným povrchem deskového pěnového izolantu, je ve všech tloušťkách stejný (energie se nikde v izolantu nemůže hromadit, to, co do dané vrstvy přiteče, musí také v ustáleném stavu odtéct). V příštím článku na toto téma ukážeme, že tato podmínka si vynutí podstatnou nelinearitu v průběhu teploty a těsnou interakci mezi oběma mechanismy, tzn. vedením tepla a sáláním.

Literatura a zdroje:

Čtěte dál na stejné téma

NEOPOR - tepelná izolace nové generace
Šíření tepla skrze bílý a šedý pěnový polystyren a jiné lehké tepelné izolanty
Šedý pěnový polystyren NeoFloor a GreyWall – izolace nové generace nově na trhu
Šedý a bílý pěnový polystyren – popis termoizolační funkce
Šedý a bílý pěnový polystyren – popis termoizolační funkce (2)
Reflexní ochrana tepelné izolace ve střechách a fasádách