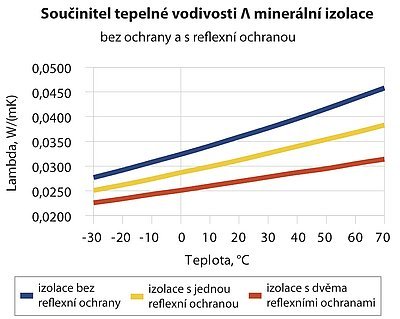
Reflexní ochrana tepelné izolace ve střechách a fasádách
Stavební tepelné izolace jsou až z 98 procent vyplněny vzduchem a při pokojové teplotě se v nich šíří teplo cca z jedné třetiny sáláním. Intenzita sálání ale roste se čtvrtou mocninou teploty. V rozsahu praktických teplot od –30 °C do 60 °C se proto mění účinnost tepelné izolace až o 30 procent. Podstatně omezit vliv sálání v izolaci a tím zlepšit její tepelněizolační vlastnosti lze pomocí reflexních fólií.
Výrobci minerálních i pěnových tepelných izolací někdy v žertu, ale s oblibou říkají, že jejich cílem je prodávat vzduch, protože ten je prý nejlepší tepelný izolant. Není to trefná argumentace. I kdyby vláknitá nebo pěnová struktura izolace dokázala úplně znehybnět vzduch, ale neclonila sálání, měla by taková izolace o tloušťce 100 mm tyto součinitele tepelné vodivosti (STV) λ:
λ = 0,389 W/(mK) při teplotě –20 °C,
λ = 0,594 W/(mK) při teplotě +20 °C,
λ = 0,864 W/(mK) při teplotě +60 °C.
Hodnoty λ se nápadně zhoršují s rostoucí teplotou. Zhoršují se i s rostoucí tloušťkou a to téměř úměrně: při tloušťce 200 mm a teplotě +20 °C je už Λ = 1,163 W/(mK). Je to tím, že klasická tepelná vodivost vzduchu se na celkovém prostupu tepla podílí několika procenty. Dominantní je zde transport tepla sáláním, ale ten se neřídí lineárním Fourierovým zákonem, v němž je STV konstantní.
Výše uvedené hodnoty byly spočteny na základě Planckova zákona upraveného pro sdílení tepla mezi rovnoběžnými rovinami o termodynamických teplotách T1, resp. T2 v kelvinech (K). Ty se počítají tak, že k teplotě ve °C připočteme 273,15. Abychom počítali STV při dané teplotě, volíme velmi malé rozestupy teplot T1 a T1, např. (20 +273,15) K a (20,1 +273,15) K, a pak dosazujeme do vztahu:
|
| (1) |
kde σ = 5,67×10-8 W/(m2K4) je Stefanova-Boltzmannova konstanta, ε1 = ε2 = 1 je bezrozměrná emisivita obou rovin, L je tloušťka vzduchové vrstvy (vzdálenost desek) a λ je „klasický” součinitel tepelné vodivosti vzduchu. Je vidět, že vzduch v tepelné izolaci sám o sobě nic neznamená. Nutnou podmínkou pro fungování izolace je, aby její vláknitá nebo pěnová struktura omezovala průchod tepelného záření.
Přibližme si to. Má-li skutečná tepelná izolace při teplotě 15 °C hodnotu STV λ = 0,035 W/(mK), na níž se podílí vzduch příspěvkem λ = 0,0255 W/(mK), potom 27 % tepla se přenáší zářením. To, že je to jen 27 %, plyne z toho, že vlákna či pěna izolace částečně pohlcují tepelné záření. Když se tepelné záření (tj. sálání) podaří v izolaci zcela odclonit, dostaneme se k tabulkové hodnotě STV na úrovni nehybného vzduchu. Ideálním prostředkem k tomu jsou reflexní fólie.
Z fyzikálního hlediska je pro reflexní fólie charakteristická velmi nízká emisivita od ε = 0,02 do ε = 0,2. Připomeňme, že je vždy 0 ≤ ε ≤ 1, u běžných povrchů je ca ε = 0,9. Ideální reflexní fólie nepropouští dopadající záření, nýbrž 100 × ε procent z něj pohlcuje a zbytek, 100 × (1 – ε) procent, odráží. Dosadíme-li např. ε1 = ε2 = 0,1 do vztahu (1), dostaneme:
λ = 0,0420 W/(mK) při teplotě –20 °C,
λ = 0,0558 W/(mK) při teplotě +20 °C,
λ = 0,0729 W/(mK) při teplotě +60 °C.
Výsledek oproti řešení bez fólie nebo s nereflexní fólií, které mají ε = 1, jsme zlepšili zhruba o 90 procent. Podíl sálání na celkovém transportu tepla se snížil cca na polovinu, vliv klasické fourierovské vodivosti vzduchu vzrostl. Výsledné hodnoty přesto nejsou nejlepší, a navíc jde o nepraktické řešení. Prostou vzduchovou mezeru ohraničenou z obou stran reflexní fólií bychom bez pomocných konstrukcí těžko realizovali, natožpak nehybnost vzduchu, jehož proudění by výsledky úplně znehodnotilo.
Vlastnosti tepelné izolace chráněné reflexními fóliemi
Pohodlnější je aplikovat reflexní fólii na jeden či oba povrchy izolačních desek nebo rohoží se stabilními rozměry a tím spojit několik výhod, které u vzduchové mezery chybějí:
- vláknitá nebo pěnová struktura izolace cloní sálání,
- vlákna či pěna zajistí nehybnost vzduchu,
- izolační desky jsou dostatečně tuhé, což zajišťuje geometrickou stabilitu celé sestavy.
Výpočtový model a předpoklady
To, že pevná složka izolace brzdí sálavý tok energie, znamená, že pohlcuje tepelné záření ve smyslu Beerova-Lambertova zákona:
|
| (2) |
Rovnice (2) říká, že sálavý tok o intenzitě I se po průchodu (nekonečně tenkou) vrstvou izolace dx zmenší o hodnotu dI. Součin k·dx lze nazvat pohltivostí vrstvy, materiálová konstanta úměrnosti k se nazývá součinitel absorpce. Čím je k větší, tím izolace víc pohlcuje tepelné záření a víc brzdí sálavý tok. Jestliže podle Planckova zákona sálá okrajová fólie o termodynamické teplotě T1 s intenzitou I = σε1T14, potom vrstva izolace dx ve vzdálenosti x pohlcuje z tohoto záření část σε1T14e–kx·k·dx. Exponenciální člen e–kx vyjadřuje pokles intenzity záření po projití od okraje k vrstvě dx ve vzdálenosti x, jak plyne z integrace (2).
Z 2. zákona termodynamiky plyne, že vrstva dx musí také teplo sálat (emitovat), a to se stejnou účinností, jako jej pohlcuje. Její pohltivost k·dx se proto číselně rovná i emisivitě. Vrstva dx o teplotě T(x) tedy sálá s intenzitou dI = σ·T4(x)·k·dx a okrajová fólie z toho pohltí část σ·T4(x)·k ε1·e–kxdx (i fólie pohlcuje i emituje se stejnou účinností ε). Výsledná bilance výměny sálavého tepla mezi fólií a vrstvou dx je:
|
| (3) |
Integrací přes tloušťku izolace, tedy od x = 0 do x = L, spočítáme intenzitu výměny sálavého tepla mezi okrajovou fólií a zbytkem izolace, označme ji jako I = ∫dI. K ní připočítáme ještě výměnu sálavého tepla, které si okrajová fólie předává s fólií na opačné straně izolace s emisivitou ε2 a teplotou T2:
|
| (4) |
a konečně i tok tepla klasickým vedením vzduchem, do něhož započítáme i dva odpory rk při přestupu tepla vedením. Pro celkový součinitel vedení tepla, který zahrnuje i sálání tepla izolací je:
|
| (5) |
|
| |
|
| (6) |
Téma: reflexní tepelné izolace
Výsledky
Pro jednodušší integraci rovnic (3) a (6) jsme uvažovali lineární průběh teploty v izolaci, což je pro velké hodnoty k a malé teplotní spády v izolaci dobře splněno. Celkový STV λ v (5) výrazně závisí na součiniteli absorpce k. Ten jsme nastavili na hodnotu k = 570 m-1 tak, aby při STV vzduchu λ = 0,0255 W/(mK), teplotě 15 °C (přesněji 15 °C na teplém a 14 °C na chladném okraji) a tloušťce izolace 100 mm bylo λ = 0,035 W/(mK), jak tomu přibližně je u skutečných izolací.
Pro k = 570 m-1 připadá na sálání 27 % z celkové vodivosti. Tepelný paprsek se přitom po 1,22 mm oslabí na polovinu. To znamená, že se v izolaci šíří sálavé teplo postupně: Izolace sice po několika mm každý tepelný paprsek téměř pohltí, ale zároveň vyzařuje nové paprsky, které šíří teplo dál.
V tab. 1 a na grafu v obr. 1 jsou výsledky výpočtů teplotní závislostí součinitele celkové tepelné vodivosti izolace λ, která je a) bez reflexní ochrany, kdy ε1 = ε2 = 1, b) s jednou ochrannou reflexní fólií o emisivitě ε1 = 0,1 a c) se dvěma reflexními fóliemi o emisivitě ε1 = ε2 = 0,1.
Na první pohled je vidět, že u izolace bez reflexní ochrany roste STV izolace rychle s teplotou. Naopak, pokud izolaci z obou stran chráníme reflexní fólií orientovanou do izolace, je teplotní růst STV pomalejší.
Zásadní ale je, že už při aplikací reflexní fólie na jedné straně izolace podstatně snížíme její STV. Při oboustranné aplikaci dokonce docílíme STV pod 0,030 W/(mK) i při extrémně vysokých teplotách.
| teplota (°C) | -20 | -10 | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| izolace bez reflexní ochrany | 0,0292 | 0,0308 | 0,0324 | 0,0341 | 0,0359 | 0,0377 | 0,0396 | 0,0416 | 0,0437 |
| odchylka od vztažné hodnoty | -16,6% | -12,0% | -7,4% | -2,6% | 2,6% | 7,7% | 13,1% | 18,9% | 24,9% |
| izolace s jednou reflexní ochranou | 0,0262 | 0,0274 | 0,0287 | 0,0299 | 0,0312 | 0,0326 | 0,0340 | 0,0354 | 0,0368 |
| odchylka od vztažné hodnoty | -25,1% | -21,7% | -18,0% | -14,6% | -10,9% | -6,9% | -2,9% | 1,1% | 5,1% |
| izolace s dvěma reflexními ochranami | 0,0234 | 0,0243 | 0,0251 | 0,0260 | 0,0269 | 0,0278 | 0,0287 | 0,0295 | 0,0305 |
| odchylka od vztažné hodnoty | -33,1% | -30,6% | -28,3% | -25,7% | -23,1% | -20,6% | -18,0% | -15,7% | -12,9% |
Reflexní fólie – nejlepší ochrana střešních izolací
Vysoké venkovní teploty až k 70 °C v tab. 1 a obr. 1 jsou zmíněny proto, že se často objevují pod střešní krytinou při celodenním letním slunečním svitu. Ochranou tepelné izolace reflexní fólií docílíme při těchto podmínkách cca 30 procentního snížení prostupu tepla do podkroví a podstatně zlepšíme pobytové podmínky.
Odrazivé povrchy orientovány do izolace
Tento model předpokládá, že jsou reflexní povrchy fólií orientovány do izolace. Odrazivá vrstva zde totiž nemůže být ochlazována (nebo ohřívána) proudícím vzduchem. A potom téměř veškeré tepelné záření vrstva odráží zpět do izolace a sama ho vyzařuje minimum. Při emisivitě ε = 0,1 je přestup zářivého tepla na reflexní vrstvě snížen na 10 %, při emisivitě ε = 0,02 na 2 %.
Opačná orientace reflexních vrstev ven z izolace je také možná, výsledky se zhorší o vliv proudění vzduchu podél „větraných” reflexních povrchů. Na druhé straně reflexní povrchy v tomto uspořádání odrážejí a tedy vůbec nepřijímají intenzivní sálaní např. z rozpálené krytiny, čímž si udržují nižší teplotu. To naopak účinnost izolace zlepšuje.
Chování izolace v extrémních teplotních podmínkách
Když nechráněná izolace přenáší velké teplotní rozdíly, je na jejím teplém okraji znatelně vyšší STV než na chladném. Efektivní hodnota, se kterou pracujeme v běžném lineárním přiblížení, leží někde uprostřed. Pokud izolaci ochráníme z obou stran reflexní fólií, docílíme toho, že se krajní hodnoty λ méně rozestoupí, ale navíc že se výrazně přiblíží k hodnotě λ nehybného vzduchu. Ukazuje to tab. 2.
| rozdíl teplot,t2→t1 | +60 °C →+25 °C | -30°→C+20 °C |
| ε1 = ε2 = 1 | λ= 0,0402 W/(mK) | λ= 0,0318 W/(mK) |
| ε1= 1 a ε2 =0,1 | λ= 0,0338 W/(mK) | λ= 0,0293 W/(mK) |
| ε1 =0,1 a ε2 = 1 | λ= 0,0353 W/(mK) | λ= 0,0273 W/(mK) |
| ε1 = ε2 = 0,1 | λ= 0,0289 W/(mK) | λ= 0,0247 W/(mK) |