Difúze a kondenzace vodní páry - difúzně otevřené konstrukce
Difúze vodní páry a tepelná izolace jsou dvě strany stejné mince. Difúze by asi zůstala ve stavební praxi i teorii zcela nepovšimnuta, nebýt toho, že difundující pára občas v konstrukci kondenzuje, a tím dělá potíže. Problematiku difúze vodní páry ve stavebních konstrukcích uvádí tento článek.
Difúze vodní páry je prostup molekul páry porézní strukturou stavebních konstrukcí z míst o vyšší koncentraci páry do míst s nižší koncentrací. Děje se jako následek spontánní tendence všech soustav zaujímat rovnovážný stav, tedy i rovnoměrnou koncentraci páry. Nepohání ji žádná fyzikální síla. Difúzi vodní páry v konstrukcích v zásadě nepotřebujeme. Spíš jsme nuceni ji trpět a činit opatření, aby difundující pára nekondenzovala. A když, tak jen krátce a málo, aby se pak vysrážená vlhkost v teplém období bezpečně odpařila.
Toto téma dnes ožilo i v souvislosti s tzv. difúzně otevřenými izolacemi a konstrukcemi. Ty kladou difundující vodní páře relativně velmi malý odpor, takže difúzní tok může být vysoký. Aby dobře fungovaly, s minimem kondenzace nebo bez ní, musejí mít kvalitní návrh.
Historie difúzně otevřených konstrukcí
Ještě nedávno byl takřka každý dům difúzně otevřený. Pak se objevily polystyrénové tepelné izolace, které špatně propouštěly vodní páru. Anebo paro- a vzduchotěsné fólie v lehkých dřevostavbách vycpaných tepelnou izolací z minerální vlny, které páru nepropouštěly vůbec. Takto izolované a fóliované stavby, přesněji stěnové konstrukce si záhy vysloužily nepřiléhavé a nelichotivé pojmenování "nedýchající". Fixovaly pocit nezdravých konstrukcí, přestože při fyzikálně dobrém návrhu byly funkční a bezpečné.
Toho využili někteří výrobci dřevostaveb a hlavně výrobci tepelných izolací z rostlinných a dřevitých vláken, kteří začali nabízet obálkové konstrukce či celé domy bez parobrzd a parozábran, kterým dali odborný název difúzně otevřené i s přesnou definicí (faktor difúzního odporu μ<5). Jejich součástí byly difúzně otevřené izolace rostlého původu použitelné i na cihlový nebo kamenný dům. V marketingové komunikaci se mluví o dýchajících konstrukcích a izolacích.
Difúzně otevřené izolace bývají dražší než ty běžné. Brouzdáním na internetu zjistíme, že většina výrobců tuto nevýhodu vyvažuje pomocí ideologie udržitelnosti s důrazem, kromě již řečeného dýchání, že jde o izolace s nulovým potenciálem globálního oteplování (GWP). Uchopitelnější výhodou je, že se nutně neaplikují spolu s parotěsnými fóliemi, jejichž provedení – zvlášť v místech komplikovaných detailů – není vždy jisté. Nehrozí tedy jejich protržení, provrtání či jiné poškození parotěsnosti při dlouhodobém užívání.
Fyzikální popis difúze
Princip je stejný jako u vedení tepla, což je jen jiný typ difúze. Obecně se řeší difúzní rovnice. Je-li u difundující stavová veličina, má difúzní rovnice v jednorozměrné reprezentaci tvar:
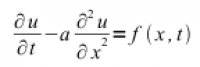
kde
u je termodynamická stavová veličina (tlak, teplota ap.),
t je čas v s,
x je prostorová souřadnice v m,
a je materiálová konstanta a
f(x,t) je zdrojová funkce.
Ve většině případů uvažujeme f(x,t) = 0, tzn. že uvnitř sledované oblasti nejsou žádné zdroje (vodní páry, tepla, chemických částic, ap.)
Tlakové pole vodní páry v konstrukci
Je-li ona stavová veličina částečný tlak vodní páry p (v Pa), dostaneme difúzní rovnici pro vodní páru:
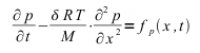
kde
p je částečný tlak vodní páry v Pa,
δ je součinitel difúzní vodivosti v s,
R = 8 314 J/(kmol K) je plynová konstanta,
T = 273,15+θ °C termodynamická teplota v K,
M = 18,015 kg/kmol je molární hmotnost vodní páry a
fp(x,t) je zdrojová funkce v Pa/s.
Součinitel ap = δRT/M o fyzikálním rozměru m2/s v rovnici (2) je obdobou součinitele teplotní vodivosti v rovnici vedení tepla. Plyne ze stavové rovnice vodní páry a je mírou rychlosti šíření vlhkostní vlny.
Zdrojovou funkci budeme zanedbávat, tzn. že položíme fp(x,t) = 0. Může se to zdát jako chyba, protože když v konstrukci dojde ke kondenzaci, může to být významný zdroj vlhkosti.
Částečný tlak vodní páry v místech kondenzace se ale už neřídí difúzní rovnicí (2), nýbrž setrvává na hodnotě částečného tlaku syté páry (ČTSVP), která závisí jen na teplotě. Úlohu difúze vodní páry s kondenzací v konstrukci proto rozdělíme na "suchou" oblast, v níž se částečná tlak vodní páry (ČTVP) řídí zákonem (2), a na "mokrou" oblast, kde je ČTSVP přibližně popsán empirickou Magnusovou rovnicí:
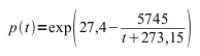
kde t je teplota ve °C. ČTSVP je nejvyšší možný tlak, který může pára při dané teplotě dosáhnout, další přírůstky páry kondenzují. V běžných pobytových podmínkách je ČTVP menší a bývá vyjadřován procentním podílem z ČTSVP při dané teplotě, kterému říkáme relativní vlhkost. Např. při 20 °C je podle (3) ČTSVP roven 2 386 Pa. Je li v místnosti skutečný ČTVP jen 1432 Pa, pak relativní vlhkost (RH od angl. relative humidity) je 1432/2 386×100 = 60 % RH.
Poznámka: Hodnota ČTSVP vůbec nezávisí na přítomnosti vzduchu. Kdybychom vpouštěli vodní páru do lahve se 100% vakuem, tak jakmile vodní pára začne na stěny lahve působit tlakem o velikosti ČTSVP podle (3), začne se v lahvi srážet rosa.
Vraťme se nyní k řešení rovnice (2). Pro praxi má největší význam řešení za ustálených podmínek, kdy se nemění teplotní a hmotnostní toky. Potom ve (2) vymizí časová derivace, tedy ∂p/∂t = 0. Je-li také fp(x,t) = 0, důvody jsme již uvedli, vznikne velmi jednoduchá obyčejná diferenciální rovnice:
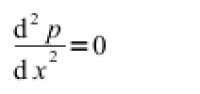
která má (pro stejnorodou vrstvu) velmi příjemné řešení p = Kx + C, kde K a C jsou neznámé konstanty. Pro okrajové podmínky p(0) = p1 a p(d) = p2 dostaneme
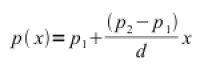
kde
d je tloušťka vrstvy v m,
x je hloubková souřadnice v m, 0 ≤ x ≤ d,
p(x) je ČTVP v Pa v hloubce x a
p1 a p2 jsou okrajové ČTVP v Pa.
Ve stavební fyzice jde o notoricky známý 1. Fourierův zákon pro ustálená teplotní pole a jim odpovídající tepelné difúzní (nikoliv sálavé) toky. Ve vrstvené (sendvičové) stěně musíme pro každou vrstvu počítat zvlášť difúzní odpor, součet difúzních odporů všech vrstev dá pak celkový difúzní odpor. Z něho a z rozdílu hodnot ČTVP na okrajích sendviče určíme ustálený hmotnostní tok vodní páry, který musí být ve všech vrstvách stejný (pára se nikde nehromadí, ani nemizí = princip kontinuity). Pro každou vrstvu i platí
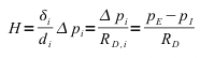
kde
H je hustota hmotnostního toku vodní páry v kg/(m2Pa),
d i je tloušťka i -té vrstvy,
Δp i = p i – p i −1 je rozdíl ČTVP na i-té vrstvě,
pI a pE jsou vnitřní a venkovní ČTVP v Pa.
RD,i je difúzní odpor i-té vrstvy v m/s,
RD = ∑RD,i je celkový difúzní odpor v m/s.
Zároveň platí, že ∑Δpi = pE – pI, z čehož snadno odvodíme hodnoty ČTVP na hranicích vrstev, tedy posloupnost pE, p1, p2, ..., pE. Při jejich znalosti pak podle (5) určíme i průběh ČTVP uvnitř vrstev.
Zatím ještě nevíme, jak velké difúzní toky můžeme očekávat. Ani jak vážný problém může nastat s kondenzací. O tom rozhodne rozdíl částečných tlaků vodní páry na obou stranách konstrukce, tzn. uvnitř domu a venku. Tab. 1 naznačuje, jak se může měnit podle venkovní teploty.
| Rozdíl částečných tlaků vodní páry uvnitř a venku Uvnitř: 20 °C, 60 % rel. vlhkosti → ČTVP = 1432 Pa | ||||||
| Venkovní teplota, °C | –25 | –15 | 0 | 15 | 20 | 30 |
| Rozdíl ČTVP Δp, Pa | –1377 | –1298 | –977 | –73 | 477 | 2212 |
Rozdíl Δp, který se ve fyzikální mluvě nazývá termodynamickým potenciálem difúze, může být při extrémních venkovních teplotách poměrně vysoký. Tab. 1 ukazuje konkrétní hodnoty Δp pro vnitřní teplotu 20 °C a relativní vlhkost 60 % RH, zatímco venku je vlhkost 80 % RH a mění se teploty. Difúzní tok je orientován z prostředí o vyšším ČTVP do prostředí s nižším ČTVP, v zimě z vnitřku ven, v horkém létě naopak.
Zóna kondenzace
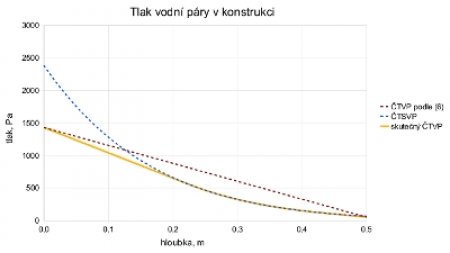
Při dostatečném rozdílu venkovního a vnitřního ČTVP Δp = pE – pI se stává, že průběh ČTVP v konstrukci daný předpisem (6) protne průběh ČTSVP spočítaného podle Magnusova vzorce (3), do kterého dosazujeme teploty v konstrukci stanovené podle 1. Fourierova zákona pro ustálené vedení tepla. Ukazuje to graf na obr. 2., který znázorňuje difúzní chování stěny z pórobetonu Porfix tloušťky 500 mm se součinitelem tepelné vodivosti λ = 0,09 W/(mK) a průměrným faktorem difúzního odporu 7,5. Teplotní spád v konstrukci je od +20 °C na vnitřním povrchu do –25 °C na venkovním povrchu. Vnitřní relativní vlhkost (RH) je 60 %, venkovní 80 % RH.
Modrá přerušovaná křivka ukazuje průběh částečného tlaku syté vodní páry podle (3), zatímco a červená přímá čára ukazuje průběh ČTVP podle (5), resp. (6). V hloubce 126 mm pod vnitřním povrchem až do hloubky 494 mm je ČTSVP menší než ČTVP. To je znamením, že ve stěně dochází ke kondenzaci.
Interval kondenzace bude ale menší než úsek od 126 mm do 494 mm, v němž je ČTSVP < ČTVP. Skutečný interval kondenzace bude jen od 224 mm do 432 mm. Snížený ČTVP v zóně kondenzace totiž způsobí, že se na teplé straně zvýší tlakový spád a na studené naopak sníží.
Proto skutečný částečný tlak vodní páry v grafické reprezentaci na obr. 2 připomíná napjatou strunu (žlutá křivka), která vybíhá na vnitřní straně z pozice p I, pak tečně splyne s křivkou ČTSVP (modrá čárkovaná křivka), chvíli ji kopíruje (žlutomodrá křivka) a pak tuto křivku tečně opustí, načež napjatá dorazí na pozici pE na venkovní straně.
Uveďme si další veličiny, související s touto stěnou, které si čtenář s uvedeným aparátem může spočítat sám:
Tlakový spád na stěně: 1377 Pa; celkový tepelný odpor: 5,62 m2K/W; celkový difúzní odpor: 2,11×1010 m/s; ekvivalentní difúzní tloušťka: 3,75 m; hmotnostní tok vstupující vlhkosti: 9,22×10–8 kg/(m2s); hmotnostní tok vystupující vlhkosti: 2,25×10–8 kg/(m2s); intenzita kondenzace: 6,97×10–8 kg/(m2s), tj. 6,02 ml/(m2den).
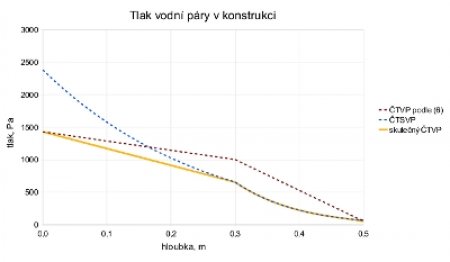
Graf na obr. 3 ukazuje parně difúzní charakteristiky stejného pórobetonu tloušťky 300 mm se zateplením tloušťky 200 mm z pěnového polystyrénu o součiniteli tepelné vodivosti λ = 0,04 W/(mK) a průměrným faktorem difúzního odporu 25. Všechny okrajové podmínky jsou stejné, jako v předešlém grafu. Tepelná izolace se projeví na tvaru křivek ČTVP z difúzní rovnice a skutečném tlaku vodní páry. Hlavní změny jsou, že se zóna kondenzace "přestěhovala" ze zdiva do izolace a že se snížil tok vstupující vodní páry i intenzita kondenzace. Důležité tepelně difúzní veličiny jsou:
Celkový tepelný odpor: 8,37 m2K/W; celkový difúzní odpor: 4,07×1010 m/s; ekvivalentní difúzní tloušťka: 7,25 m; hmotnostní tok vstupující vlhkosti: 6,14×10–8 kg/(m2s); hmotnostní tok vystupující vlhkosti: 1,01×10–8 kg/(m2s); intenzita kondenzace: 5,13×10–8 kg/(m2s), tj. 4,43 ml/(m2den).
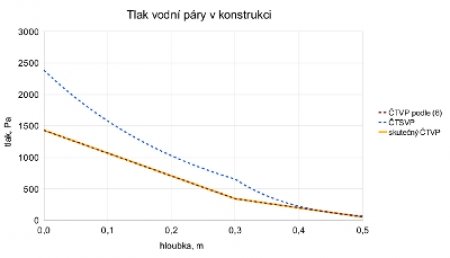
Graf na obr. 4 ukazuje difúzní charakteristiky stejného pórobetonu tloušťky 300 mm se zateplením tloušťky 200 mm z minerální vlny o součiniteli tepelné vodivosti λ = 0,04 W/(mK) a průměrným faktorem difúzního odporu 3. Tepelná izolace se opět projeví na tvaru křivek ČTVP z difúzní rovnice a skutečném tlaku vodní páry. Všechny okrajové podmínky jsou stejné, jako v předešlém grafu.
V tomto případě vysoce difúzně propustná tepelná izolace odvede veškerou vstupující vodní páru ven, aniž by při takto drsných podmínkách (venkovní teplota -25 °C) došlo v celé sestavě ke kondenzaci. Je to ale jen o "fous", na grafu křivky v blízkosti venkovního povrchu zdánlivě splývají. O to víc je nutné udělat kontaktní omítku na izolaci vysoce difúzně propustnou. Odpovídající tepelnědifúzní veličiny jsou:
Celkový tepelný odpor: 8,37 m2K/W; celkový difúzní odpor: 1,6×1010 m/s; ekvivalentní difúzní tloušťka: 2,85 m; hmotnostní tok vstupující vlhkosti: 8,6×10–8 kg/(m2s); hmotnostní tok vystupující vlhkosti: 8,6×10–8 kg/(m2s); intenzita kondenzace: 0,00×10–8 kg/(m2s), tj. 0,00 ml/(m2den).
Veličiny a jednotky "difúzních" výpočtů
Základní jednotky parní difúze jsme už zmínili. Je to součinitel difúze neboli difúzní vodivosti daného materiálu δ v sekundách, difúzní odpor RD = d/δ v jednotkách m/s pro vrstvu tloušťky d z daného materiálu a hustota hmotnostního toku při difúzi vodní páry H v kg/(m2Pa).
Dále se používá faktor difúzního odporu μ, což je bezrozměrná veličina, která říká, kolikrát daný materiál propouští vodní páru hůře ve srovnání se vzduchem. Platí
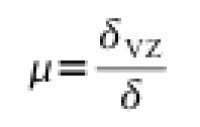
kde μ je faktor difúzního odporu, δVZ = 0,178×10–9 s je součinitel difúze vodní páry při 0 °C a δ je součinitel difúze daného materiálu.
Poslední užívanou veličinou je ekvivalentní difúzní tloušťka SD, která udává, jaká tloušťka vzduchu odpovídá svým difúzím odporem dané vrstvě, nátěru nebo fólii. Platí
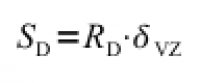
kde SD je ekvivalentní difúzní tloušťka daného materiálu v m, RD je jeho difúzní odpor v m/s a δVZ = 0,178×10–9 s je součinitel difúze vodní páry.
Téma: Difúze a kondenzace
Kam dál?
Difúze vodní páry - veličiny, hodnoty a jednotky
Difúze vodní páry v konstrukci