Vzduchová mezera jako podstatná součást zateplení budov

Nejsilnější teplosměnné děje nejen v přírodě, ale i ve stavbách realizuje sálání. Účinná tepelná izolace musí téměř zcela přerušit nejen „klasické“ teplosměnné děje - proudění a vedení tepla, ale hlavně sálavý tok tepla. Nejlepším řešením jsou reflexní tepelné izolace ve vzduchové mezeře v roli tepelněizolačního souvrství domu.

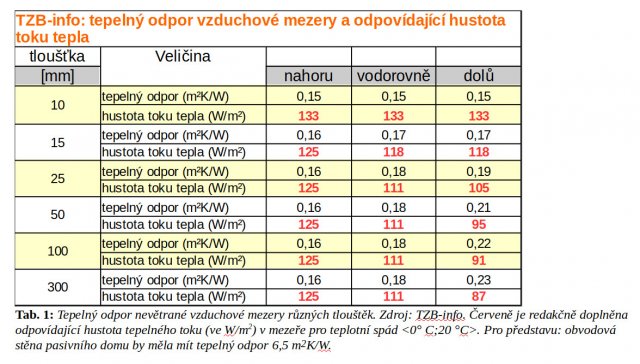
Dnešní stavebnictví si s mezerou neví moc rady. Zná jen klasickou izolaci, řeší jen zimu a za vyšší energetickou náročností vidí jen zastaralá či špatná stavební řešení. Na https://www.tzb-info.cz/ je tabulka tepelných odporů vzduchových mezer o tloušťkách od 10 do 300 mm podle ČSN EN ISO 6946 (730558). Tabulku jsme obohatili o hustotu sdílení tepla při teplotním spádu <0°C; 20°C> mezi chladným a ohřátým okrajem mezery (červená čísla).

Tab. 1 říká, že mezera v roli tepelné izolace je hloupost. Ať je jakkoli tlustá, její tepelný odpor R je na hony vzdálen termoizolační obálce pasivního domu (cca R = 6,5 m²K/W). Odtud je už jen krok k myšlence, že každou vzduchovou mezeru je nejlépe vycpat tepelnou izolací.

Jenže tak tomu není. Ukažme si, že hlavním teplosměnným dějem v mezeře je sálání a že jeho odcloněním reflexními povrchy zvýšíme tepelný odpor prázdné mezery až vysoko nad možnosti její „vycpávky“ běžnou tepelnou izolací.

Tepelné vlastnosti vzduchové mezery

Článek „Tepelný odpor vzduchové mezery… “ v [1] ukázal, že výpočet podle ČSN EN ISO 6946 vyplývá z neznalosti fyzikálních dějů v mezeře a nepopisuje skutečnost. To ukázala i praxe…

Teplo ve stavebnictví

Základem dnešní stavební fyziky tepla je proudící vzduch a jeho teplota. Jako bychom stéle žili v časech německých vědců Grashofů, Nusseltů a Prandtlů, kteří se prouděním sice…

Sálavý tok tepla v mezeře

Pracujme s prázdnou vzduchovou mezerou, jejíž okraje mají teplotu 0 °C a 20 °C. A nechť je v ní jediným teplosměnným dějem sálání. To se realizuje dvěma způsoby:

1. Sdílení sálavého tepla mezi okraji mezery: Ze Stefanova - Boltzmannova zákona plyne, že při řečených okrajových teplotách zde sálání realizuje prostup tepla o intenzitě 103 W/m². To je víc než 77 % celkového prostupu tepla mezerou. Sálaní jasně dominuje.


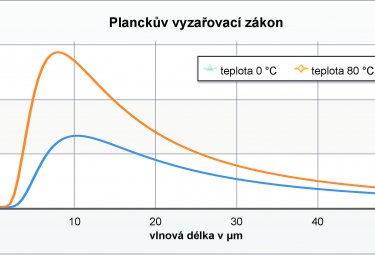
2. Sdílení sálavého tepla mezi okraji mezery a jejím vnitřkem: Z jiného základního zákona (Planckova) plyne, že energetická hodnota a vůbec sama existence tepelného záření závisí jen na teplotě. Z tohoto pohledu je prostor mezery identický s tělesem o teplotě 10,4 °C (= 4. odmocnina z průměru 4. mocnin termodynamických teplot okrajů mezery, vyjádřená ve °C). Toto „prostorové těleso“ inkasuje na teplé straně zisk 51,5 W/m² a tutéž dávku na chladné straně odvádí. Tento děj, který stavební fyzika nezná, znamená významné zvýšení role sálání (a potlačení vlivu vedení a proudění tepla) v celkovém prostupu tepla mezerou. A dále pokles (byť asi mírnější) celkového tepelného odporu mezery.

Zářivá architektura budov

Oficiální stavební tepelné výpočty stojí na vzduchu a jeho teplotách. Avšak hlavním nositelem energie je horké Slunce a studený vesmír, dva sálavé energetické zdroje působící…

Termoreflexní izolace

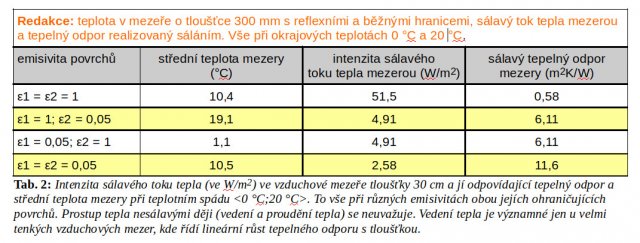
Velké sálavé toky energie ve vzduchové mezeře lze dovést téměř k nule pomocí termoreflexních okrajů mezery. Říká to Tab. 2, v níž jsou intenzity sálavého toku tepla v mezeře libovolné tloušťky, jejíž okraje mají čtyři možné kombinace emisivit ε = 1 a ε = 0,05.

Popis reflexní izolace

1. Tato izolace pracuje s celým prostorem mezery, kterou ohraničuje. Běžná izolace (EPS, MW) naopak účinkuje jen uvnitř sama sebe: Do mezery 30 cm silné musíme vložit běžnou izolaci stejné tloušťky, abychom docílili tepelného odporu R = d/λ = 0,3/0,04 = 7,5 m²K/W. Bez izolace má vzduchová mezera tepelný odpor jen na úrovni 0,19 m²K/W (viz tab. 2).

Když mezeru necháme prázdnou, jen ji jednostranně ohraničíme reflexí o emisivitě ε  = 0,05 (fólie Sunflex), výsledkem je R = 6,1 m²K/W (viz tab. 2). Při tloušťce mezery 30 cm to dává součinitel tepelné vodivosti λ = 0,049 W/(mK). Oboustranné reflexní ohraničení stejné mezery dává R = 11,6 m²K/W a λ = 0,026 W/(mK).

2. To, že reflexní izolace brzdí sálavý prostup tepla, ještě neznamená, že mezi dvěma reflexními povrchy zmizí prostorové sálání. To existuje vždy a jeho teplota se rovná teplotě T_P z rovnice (1).

Teplotní plato

Uvnitř silnějších mezer ohraničených reflexí může vzniknout teplotně méně strmá až ekvitermní centrální vzduchová vrstva, čili teplotní plato. To je výslednicí sdílení tepla mezi vzduchem a sáláním v mezeře. Pro teplotu TP platí:

Sálání, jež má všude v mezeře stejnou teplotu TP, ohřívá vzduch v sousedství chladného okraje a naopak ho chladí v sousedství teplého okraje mezery. U silnějších mezer to vede ke vzniku centrální vzduchové vrstvy o stejné teplotě (teplotní plato). Skrze plato se odehrává jen sálavý tok tepla; proudění a vedení tepla tu nemá potenciál. Sálavý teplosměnný děj lze pak snížit až téměř k nule vysokou termoreflexí okrajů mezery (tj. ε₁→0 a/nebo ε₂→0).

Tvrzení: Tepelný odpor stavební termoizolační vrstvy, např. na bázi pěnového polystyrénu, je při tloušťce 300 mm na úrovni 7,5 m²K/W. Když tutéž tloušťku realizujeme jako souvrství vzduchových mezer a reflexních fólií, získáme tepelný odpor 15 m²K/W i více.

Řízení teploty

Existují stížnosti na vysoké teploty pod střechou z tmavé krytiny, kterou letní slunce rozpálí i nad 75 °C. Tato teplota generuje sálavý tok tepla do větrané mezery s intenzitou přes 850 W/m², který má „hravě“ odvětrat vzduchová mezera pod krytinou. Jenže to by v ní musel proudit vzduch s rychlostí alespoň 10 m/s. Což se neděje.

Lavinu tepla od sluncem rozpálené střešní krytiny lze úspěšně řešit pomocí reflexních povrchů, ať už jsou realizovány folií nebo nátěrem. Při jejich správném návrhu a provedení významně snížíme nejen teplotu ve větrané vzduchové mezeře pod krytinou, ale i prostorovou teplotu pod střechou a v celém domě. Princip reflexní tepelné ochrany je jednoduchý:

1. termoreflexní povrch odráží (téměř) veškeré tepelné záření, které naň dopadá;
2. termoreflexní povrch, ať už jakkoli ohřátý, sálá do okolí jen minimum svého tepla.

V případě střechy lze pod krytinu umístit, řekněme, jednostrannou reflexní fólii tak, aby termoreflexe mířila do větrané mezery. Nebo lze spodní stranu krytiny natřít stříbrným nátěrem (typu Reflexol) s minimální emisivitou. Objeví-li někdy stavitelství výjimečnou sílu reflexe a sálání, objeví se i systémová termoreflexní řešení střech, fasád a domů.

Historie sálání

Sálání je prvotní teplosměnný děj, který „úřaduje“ už od samého vzniku Vesmíru před cca 14 miliardami let. Jde o elektromagnetické záření s typickým spektrálním rozložením, které závisí jen na teplotě a které v podobě fyzikálního vzorce popsal roku 1900 Max Planck pod názvem Záření černého tělesa. Aby se vyhnul tzv. ultrafialové katastrofě, která je v rozporu s realitou, vyslovil Planck předpoklad, že energie tohoto záření je přenášena jen po konečně velkých kvantech o velikosti E = hν, kde h = 6,626...×10⁻³⁴ J⋅s je konstanta (dnes Planckova) a ν je frekvence záření.

Vědec pokládal kvantování a konstantu h jen za matematický obrat, který zaručil souhlas teorie s experimentem. Avšak v roce 1905 zjistil Albert Einstein, že jím studovaný fotoelektrický jev vysvětluje právě hypotéza Maxe Plancka. A později Einstein odůvodnil Planckovu hypotézu studiem fotoelektrického jevu. Výsledkem bylo roku 1918 udělení Nobelovy ceny Maxi Planckovi za vyzařovací zákon a později (1921) Albertu Einsteinovi za fotoelektrický jev.

Závěr

Běžné tepelné izolace nabízejí součinitel tepelné vodivosti cca λ = 0,04 W/(mK) a jeho významný růst s teplotou. Kvalitní termoreflexní souvrství pak nabízejí λ ≤ 0,01 W/(mK). I u nich klesá tepelná izolace s teplotou, ale téměř bezvýznamně kvůli zhoršení její slabé vodivostní složky. Nízkoemisivní bílé a reflexní povrchy navíc chrání naše stavby před extrémními sálavými jevy, hlavně přímým osluněním a sálavým působením ledové zimní oblohy.

Teplota záření a teplota vzduchu v místnostech

Norma ČSN EN ISO 6946 nepřímo říká, že teplota vzduchu v uzavřené místnosti, jejíž stěny, podlaha, strop, okna, dveře ap. mají různé teploty, se vyrovnává jen prouděním vzduchu.…

Téma: reflexní tepelné izolace

Literatura a zdroje

• [1] TZB-info: Tepelný odpor nevětrané vzduchové mezery různých tlouštěk.
• [2] Hejhálek, Jiří: Tepelné záření a navrhování reflexních fólií do staveb, Vega společnost s ručením omezeným, 2014.