Termoreflexní izolace a fólie. Princip (či tajemství) jejich účinnosti

Autor: Jiří Hejhálek Zdroj: Stavebnictví a interiér 1/2012 Fotografie: Archiv firmy Kontakt: Vega společnost s ručením omezeným

Reflexní či termoreflexní izolace se začínají v praxi stále více uplatňovat. Jejich základem, jak neúplně napovídá název, je odrážení tepelného záření. Správný stavební návrh by měl počítat s konvenční i s reflexní tepelnou izolací a podle povahy stavby obě vhodně kombinovat. K tomu často chybí dostatečný vhled do principů sálání a reflexe tepla.

Pokud jde o konvenční izolace, tam se zdá být znalost základních principů lepší. Až na "drobnost", že asi 1/3 ustálených tepelných toků se v běžných vzdušných izolacích děje sáláním. Vzorce tepelných výpočtů, které jsou odvozeny z difúzní rovnice, však sálavé děje nezachycují. Nezachycují tedy ani to, že sálávé teplo se šíří rychlostí světla a na velkou vzdálenost, zatímco difúzí, tedy vedením, teplo postupuje velice pomalu a lokálně – od molekuly k molekule, bez „přeskakování“. To může mít vliv na možná až výrazně horší chování vzdušných izolací zejména v neustálených podmínkách.

Co jsou termoreflexní izolace

Základem reflexních izolací je několik mm silná bublinová či pěnová vrstva, která je pokovená z jedné či obou stran velmi tenkou vrstvou hliníku. Složením několika takových jednotek vznikne vícevrstvá reflexní izolace. Reflexní izolace nejlépe účinkují v kombinaci se vzduchovými mezerami, ve kterých díky své reflexi a emisi tepelného záření snižují sálavou složku při prostupu tepla až na 10 % i níže.

Méně známé je, že když reflexní povrch ohraničuje vzdušnou izolaci, např. desku pěnového polystyrénu, podstatně v ní sníží velikost sálavé složky − zejména v jejích okrajových vrstvách. Fakticky to znamená snížení součinitele tepelné vodivosti (lambdy) izolace. U tlouštěk izolace cca 1 cm a menších až na hodnotu lambdy vzduchu, tedy z hodnoty 0,040 W/(mK) až na 0,025 W/(mK).

Základní tepelné vlastnosti termoreflexní fólie

Je to její tepelný odpor a "sálavé" povrchové vlastnosti – reflexivita a emisivita. Obě dokáží v blízkosti reflexního povrchu podstatně omezit sálaní a tím zlepšit tepelněizolační vlastnosti vzduchu i tepelných izolací.

Reflexivita

Světelné nebo tepelné (infračervené) záření, které dopadá na lesklý povrch fólie, se z větší části odrazí nazpět ke zdroji, zbytek je fólií pohlcen. Pohlcené záření se ve fólii změní v teplo. Poměr intenzity odraženého záření a záření, které na povrch dopadá, je reflexivita, značíme ji symbolem r. Je to bezrozměrné číslo nabývající hodnot v intervalu (0;1), u běžných reflexních fólií mezi 0,8 až 0,9. Číslo a = 1– r vyjadřuje pohltivost záření fólií. Obě veličiny jsou hůře měřitelné v oblasti infračervených vln s vlnovou délkou kolem 10 mikrometrů, které odpovídají sálání těles.

Emisivita

Jde o málo názornou veličinu, neboť sálání těles o pokojových teplotách (a chladnějších) nedokážeme vidět a ani jinak vnímat. Cítíme i vidíme ovšem sálání horkých těles, např. uhlíků v ohni. Nebo záření Slunce, tedy tělesa ohřátého na 5 500 °C, jehož část cítíme jako teplo a jinou vidíme jako světlo.

Ve skutečnosti sálají nejen horká tělesa, ale všechna, i velmi chladná. Čím chladnější těleso, tím je záření slabší a méně viditelné či vnímatelné. Záření těles pod 500 °C již lidské oko nevidí a sálání těles o pokojové teplotě a nižší naše smysly registrují jen nepřímo nebo vůbec. Touto problematikou se v 18. a 19 . století zabývali vědci Gustav Kirchhoff, Wilhelm Wien, Josef Stefan, Ludwig Boltzmann a konečně Max Planck. Právě Planck formuloval roku 1900 přesný popis tepelného záření, platný dodnes. Z něho vyplynuly již dříve publikované empirické poznatky:

I) Stefanův-Boltzmannův zákon, který říká, že tzv. černé těleso sálá s intenzitou (hustotou zářivého toku), která je úměrná 4. mocnině jeho termodynamické teploty:

(W/m²)

(1)

kde σ = 5,67·10^–8 W/(m²K⁴) je konstanta.

II) Wienův posunovací zákon, který říká, že součin vlnové délky, na kterou připadá maximum intenzity vyzařování černého tělesa při termodynamické teplotě T, a této teploty je konstantní.

(W/m²)

(2)

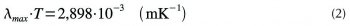
III) Kirchhoffův zákon, který uvádí relaci mezi emisivitou a pohltivostí tepelného záření. Černé těleso pohlcuje z definice veškerou zářivou energii, která na něho dopadne. Jeho poměrná pohltivost je jedna. Reflexní těleso odráží poměrnou část r dopadajícího záření a pohlcuje zbytek, tzn. poměrnou část a = 1 – r. Zákon říká, že toto těleso sálá s emisivitou , která se číselně rovná jeho součiniteli absorpce, tedy ε = a.

(W/m²)

(3)

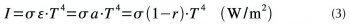
Gustav Kirchhoff své tvrzení dokázal pomocí 2. zákona termodynamiky. Pro reflexní techniku je to klíčový fakt. Pokud např. sluneční paprsky rozpálí střešní krytinu na 60 °C, sálá krytina do střechy s intenzitou 700 W/m². Přiložíme-li tenkou reflexní fólii kontaktně na spodní stranu krytiny tak, aby reflexní vrstva mířila do větrané mezery, potom těsný kontakt krytiny s fólií zřejmě zajistí, že se i reflexní povrch fólie ohřeje také na téměř 60 °C. Protože má ale fólie emisivitu ε = 1 – r = 0,1, bude vyzařovat jen s intenzitou 700·0,1 = 70 W/m². A to už je pořádný rozdíl! Intenzity sálání černých těles (= sálavých či nereflexních) při různých teplotách ukazuje tabulka.

Následující příklady znázorňují použití uvedených poznatků.

Tepelný odpor a prostup tepla pro vzduchovou mezeru

Mějme vzduchovou mezeru tloušťky w, ohraničenou z obou stran deskami o tepelném odporu R_D. Tepelný odpor R celé sestavy je R = 2·R_D + R_M a součinitel prostupu tepla podle stavební tepelné normy (pro svislou stěnu oddělující vnitřní a venkovní prostředí) je

(W/m²)

(4)

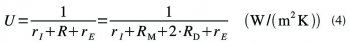
kde R_M je tepelný odpor vlastní mezery, r_I = 0,13 m²K/W je přestupový odpor na vnitřní straně konstrukce a r_E = 0,04 m²K/W přestupový odpor na venkovní straně.

Nejvíc zajímavý je odpor vlastní vzduchové mezery R_M. Ten se skládá z nesálavého odporu R_K a k němu paralelnímu "odporu" R_S, který reperezentuje sálavou složku. Pak platí

(W/m²)

(5)

Použijeme-li místo tepelných odporů jejich převrácené hodnoty, tj. a_M = 1/R_M, a_K = 1/R_K a a_S = 1/R_S, které mají fyzikální význam součinitelů prostupu tepla, dostane vzorec tvar

(W/m²)

(6)

A) Odpor vzduchové mezery R_M pro sálavé povrchy. Klasická, nesálavá složka prostupu tepla a_K je rovna reciproké hodnotě nesálavého tepelného odporu R_K vzduchové mezery a má tvar

(W/m²)

(7)

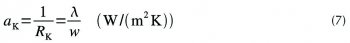
kde λ je součinitel (čisté) tepelné vodivosti vzduchu. Při střední teplotě 10 °C, kdy je λ = 0,0251 W/(mK), a tloušťce mezery 0,1 m je a_K = 0,250 W/(m²K) a R_K = 4 m²K/W.

Co se týče sálavé složky R_M, předpokládejme, že povrch desek ohraničujících z obou stran vzduchovou mezeru má ε → 1. Běžné desky mají cca ε = 0,90 až 0,98. Sálavou složku prostupu tepla mezerou spočítáme ze Stefanova-Boltzmannova zákona. Výpočet se zjednoduší, je-li mezera mezi deskami malá ve srovnání s velikostí desek, což je v konstrukcích dobře splněno.

Při teplotě t₁ = 20 °C sálá vnitřní deska s intenzitou I₁ = σ(20 + 273,15)⁴ = σT₁⁴ = 419 W/m², kde T₁ je termodynamická teplota povrchu vnitřní desky orientovaného do mezery. Protilehlá deska na studené, venkovní straně, veškeré toto sálání pohltí. Venkovní deska však také sálá. Je-li její teplota t₂ = 0 °C, sálá pak proti vnitřní desce výkon I₂ = 316 W/m². Rozdíl I₂ –I₁ = 103 W/m² je skutečná hustota toku sálavého tepla mezi deskami, tzn. sálavá složka prostupu tepla mezerou I_S:

(W/m²)

(8)

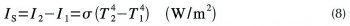
V klasické stavební tepelné technice, která vychází z difúzní rovnice (pro vedení tepla), se počítá tepelný odpor jako podíl R = ΔT/I. Vzorec lze formálně použít i pro sálavou složku a zavést "sálavý" tepelný odpor R_S vzduchové mezery ohraničené sálavými povrchy:

(W/m²)

(9)

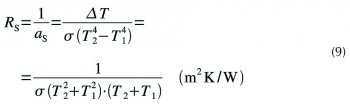
Dosazením příkladných hodnot získáme R_S = 20/(419–316) = 0,194 m²K. Celkový odpor, který zahrnuje obě paralelně působící složky, je pak 0,185 m²K/W. Vidíme, že nám sálání zcela znehodnotilo příjemně vysoký konvenční tepelný odpor R_K = 4 m²K/W. Celkový tepelný odpor R vzduchové mezery, má pak tvar

(W/m²)

(10)

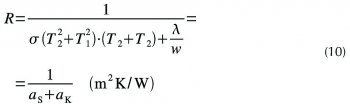
Odvodili jsme ho, podobně jako numerický výpočet, jako výslednici paralelně účinkujících odporů R_K a R_S anebo pomocí vztahu R_M = ΔT/(I_S+I_K).

A) Odpor vzduchové mezery R_M pro nesálavé povrchy. Pojem nesálavé povrchy budeme vztahovat na reflexní povrchy, jak je známe zejména u termoreflexních fólií. Ty, jak víme, odrážejí přibližně 9/10 dopadajícího záření a zbytek pohlcují. Stejný podíl, jaký pohlcují, fólie podle Kirchhoffova zákona také vyzařují a to z celku, kterým je intenzita sálání černého tělesa σT⁴. Reflexní, tzn. nesálavý povrch s odrazivostí r má tedy pohltivost a = 1 – r, která je rovna emisivitě ε. Intenzita jeho sálání je aσT⁴ = εσT⁴.

Paprsek vyzářený od vrstvy 1 o energii vyznačené červeně se odráží mezi reflexními povrchy. Při každém odrazu od vrstvy (2) paprsek část energie předá. Takto předává vrstva 1 sálavou energii vrstvě 2. Celkový tok sálavé energie mezi povrchy ukazuje vzorec (12).

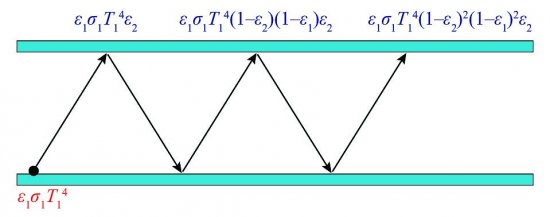
Upravme vzduchovou mezeru tak, že obě okrajové desky potáhneme tenkou reflexní vrstvou o emisivitách ε₁ a ε₂. Povrch o emisivitě ε₁ bude sálat s intenzitou ε₁σT⁴, protilehlá plocha, jejíž poměrná pohltivost je a₂ = ε₂, pohltí část ε₂ε₁σT⁴ a zbytek (1–ε₂)ε₁σT⁴ odrazí. Odražená část se po dalším odrazu o první plochu zeslabí na (1–ε₁)(1–ε₂)ε₁σT⁴ a dopadne opět na plochu 2. Ta z ní pohltí část ε₂(1–ε₁)(1–ε₂)ε₁σT⁴ a část (1–ε₂)²(1–ε₁)ε₁σT⁴ odrazí. Atd. Znázorňuje to obr. 1. Z původního paprsku ε₁σT⁴, který emitovala plocha 1, nakonec absorbuje plocha 2 část, kterou lze zapsat jako

(W/m²)

(11)

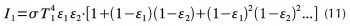
Nekonečná řada v hranaté závorce je geometrická řada s kvocientem (1–ε₁)(1–ε₂) < 1, jejíž součet je konečný a rovný, jak se učí ve středoškolské matematice, hodnotě 1/(ε₁+ε₂–ε₁ε₂). Stejný postup opakujeme se sáláním plochy 2 a po malé úpravě dostaneme velikost sdílení sálavého tepla mezi oběma nesálavými (nízkoemisivními) deskami:

(W/m²)

(12)

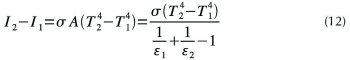
kde A = 1/(1/ε₁+1/ε₂–1) je součinitel vzájemného sálání. Všechny vzorce, které jsme odvodili pro sdílení tepla mezi sálavými povrchy, budou popisovat sdílení tepla i mezi nesálavými povrchy s emisivitami ε₁ a ε₂, jestliže místo součinitele σ použijeme součinitel σA.

Obr. 2: Tepelný odpor vzduchové mezery v závislosti na její tloušťce. Ohraničení mezery je sálavé (ε₁ = ε₂ = 1 – modrá křivka), polosálavé (ε₁ = 1; ε₂ = 0,1 – červená křivka) a nesálavé (ε₁ = 0,1; ε₂ = 0,1 – žlutá křivka). Teplotní spád 0 °C až 10 °C.

Tepelné vlastnosti vzduchových vrstev s reflexními fóliemi

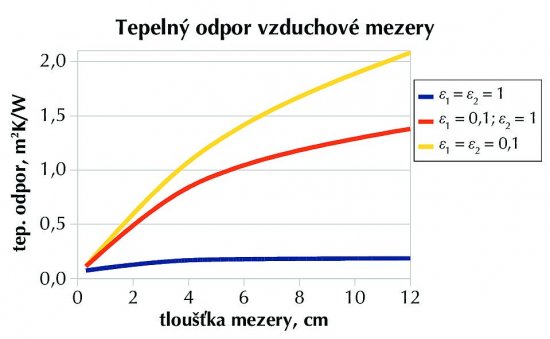
Výsledky našich úvah ukazují grafy na obrázcích 2 a 3, které znázorňují závislost tepelného odporu R_M a součinitele tepelné vodivosti λ mezery na její tloušťce a na emisivitách jejích ohraničujících desek. Zkoumavý pohled na oba grafy říká, že tu něco není v pořádku.

• Tepelný odpor u vysoce sálavých okrajů s rostoucí tloušťkou téměř nestoupá (obr. 2 - modrá křivka). V případě nesálavých nelineárně roste s tloušťkou, u větších tlouštěk se růst zpomaluje (obr. 2 - červená a žlutá křivka).
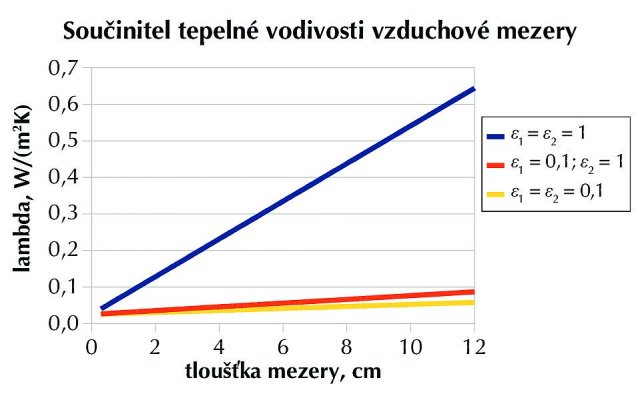
• Nezvyklá je i závislost součinitele tepelné vodivosti na tloušťce mezery, obr. 3. V případě sálavých okrajů velmi strmě a téměř lineárně roste se zvětšující se tloušťkou. V případě nesálavých okrajů růst velmi pozvolný.

K tomuto výsledku jsme došli proto, že jsme do formalismu, který přirozeně plyne z řešení difúzní rovnice pro vedení tepla, vecpali efekty zářivých dějů, které v principu nejsou difúzní povahy. Proto tu není lambda konstantní, zato tepelný odpor se konstantě může blížit.

Obr. 3: Součinitel tepelné vodovosti vzduchové mezery v závislosti na její tloušťce. Ohraničení mezery je sálavé (ε₁ = ε₂ = 1 – modrá křivka), polosálavé (ε₁ = 1; ε₂ = 0,1 – červená křivka) a nesálavé (ε₁ = 0,1; ε₂ = 0,1 – žlutá křivka). Teplotní spád 0 °C až 10 °C.

S klesající tloušťkou mezery klesá podíl sálavé složky prostupu tepla. Nesálavé, čili reflexní okraje navíc sálavou složku výrazně odcloní. Ukazuje to tab. 2. Při tloušťce mezery 1 cm a sálavých okrajích mezery je dosahuje podíl sálavé složky 67 % a součinitel lambda má hodnotu 0,077 W/(mK). Nesálavé okraje (ε₁ = 0,1; ε₂ = 0,1) zredukují sálavou složku na 9,8 % a lambda tak klesne 0,028 W/(mK).

Toho využívají výrobci reflexních bublinových nebo pěnových fólií, které při tloušťce od 3 do 5 mm s reflexním pokovením po obou stranách dosahují běžně součinitele lambda 0,026 až 0,028 W/(mK). Tyto fólie lze vrstvit do sestav o tloušťce několik cm při zachování vynikající úrovně lambdy.

Přibližně totéž, co platilo pro vzduchové mezery, platí i pro vrstvy vysoce lehčených tepelných izolací, jejichž příkladem je pěnový polystyrén. Až 98 procent jeho objemu tvoří vzduch, a proto lze logicky očekávat, že se transport tepla tímto materiálem realizuje i sáláním.

Sálaný paprsek v tomto materiálu ale urazí cca 2 až 3 mm a je pevnou strukturou pěny pohlcen; pěna samozřejmě, jako každá hmota, také záření emituje. Reflexní fólie, která kontaktně ohraničuje vrstvu pěnového polystyrénu, přeruší sálavý tok, který vstupuje či vychází z izolace. Výsledkem je snížení hodnoty součinitele tepelné vodivosti; při vrstvě o tloušťce několik mm až na hodnotu lambdy vzduchu 0, 0251 W/(mK).

Kontakty:
Vega společnost s ručením omezeným
Akad. Heyrovského 1178, 500 03 Hradec Králové 3
Tel.: +420 495 518 802
Fax: +420 495 518 804
E-mail: vegavega.cz

Diskuze a dotazy

Nejnovější články ze stejného zdroje

• Mezinárodní konference Nekonvenční zdroje elektrické energie se blíží
• Úvodník 04/2012
• Výrobek roku 2012 zná vítěze
• Veletrhy fensterbau/frontale a HOLZ-HANDWERK 2012 za námi
• Významné výročí narození architekta Pavla Janáka

Tepelná izolace

Polyuretanové sendvičové panely

9. 5. 2012 | Ing. Petr Chocholouš (Stavebnictví a interiér 4/2012)

Společnost PSP izoterm patří mezi přední zpracovatele tvrdé polyuretanové pěny v České republice. Vyrábí tvarové díly a sendvičové panely, které nacházejí uplatnění v mnoha průmyslových oblastech například ve stavebnictví, potravinářském a automobilovém průmyslu.

Bez reakcí čtenářů, 0 hlasů

Sanace a modernizace zateplení ETICS

6. 5. 2012 | Jiří Hejhálek) (Stavebnictví a interiér 4/2012)

Vnější kontaktní zateplovací systémy (VKZS nebo anglický ekvivalent ETICS) jsou montovány v Evropě již od 50. let minulého století, v České republice pak od 90. let. Mnohaletá zkušenost ukazuje, že pro jejich dlouhodobou životnost je nutná nejen kvalitní odborná montáž, ale také průběžné ošetřování a údržba tak, jak jsme zvyklí u klasických fasád.

Bez reakcí čtenářů, 1 hlas

Značení izolace z asfaltových izolačních pásů

16. 4. 2012 | Ing. Jan Plachý, Ph.D.) (Stavebnictví a interiér 2/2012)

Jedním z parametrů výběrů hydroizolace z asfaltových pásů je jejich tloušťka. Běžnou zvyklostí je obsažení tloušťky pásu v jeho obchodním názvu nebo označení. Hodnoty obsažené v názvu však vždy nemusí znamenat jeho tloušťku. Tento článek popisuje a vysvětluje jednotlivá čísla a písmena v názvu nebo označení asfaltového pásu.

Bez reakcí čtenářů, 0 hlasů

Pěnové sklo REFAGLASS – nový trend ve stavebních materiálech

23. 3. 2012 | Kolektiv autorů (Stavebnictví a interiér 3/2012)

Pěnové sklo REFAGLASS společnosti RECIFA a.s. je nový termoizolační materiál, který lze využít v mnoha oblastech stavebnictví. Zajímavou realizací se stala oprava balkónů na objektu bývalého Ústavu šlechtičen na Pražském hradě.

Bez reakcí čtenářů, 0 hlasů