Setrvačnost vnitřní povrchové teploty obvodových konstrukcí

V našich článcích se často zmiňujeme o významu takzvané relaxační doby (τ) zdiva, na základě které lze kvantitativně hodnotit zdivo z hlediska jeho tepelně akumulačních vlastností a teplotní setrvačnosti. V dnešním příspěvku se na problematiku tepelné akumulace a teplotní setrvačnosti zdiva podíváme podrobněji.

Modelový příklad, na kterém bylo v jednom z předchozích článků ilustrováno chladnutí zdiva (např. po odpojení otopné soustavy), je jednoduchý: uvažujeme chladné období, kdy je venkovní teplota nižší než vnitřní.V ustáleném (stacionárním) stavu je rozdíl vnitřní a vnější povrchové teploty zdiva udržován na konstantní hodnotě určené výkonem otopné soustavy a tepelným odporem zdiva. Tepelný tok, který do zdiva na vnitřní straně vstupuje, pak se stejnou intenzitou na jeho vnější straně vystupuje.

Odpojení otopné soustavy se projeví tak, že na vnitřní straně tepelný tok ustane, zatímco na vnější straně pokračuje - zpočátku s nezměněnou intenzitou, která však postupně klesá. Výsledkem tohoto nestacionárního děje je postupné chladnutí vnitřních částí zdiva, zatímco jeho venkovní povrch je při konstantní venkovní teplotě konstantní.

Jednovrstvé konstrukce - Stacionární definice relaxační doby

Jako »nulté přiblížení« byla v [1] definována relaxační doba na základě modelu, podle něhož tepelný výkon, který na vnější straně po dobu τ z konstrukce uniká, způsobí ochlazení vnitřního povrchu konstrukce, jehož velikost za stacionárních podmínek závisí na tepelné kapacitě jednotkové plochy a tepelném prostupu konstrukce. Pro malé hodnoty dt a krátké časy τ potom podle [1] platí:

kde ΔT je rozdíl vnitřní a vnější teploty. Konstanta úměrnosti 1/τ₀, je převrácená hodnota relaxační doby τ₀, která má fyzikální rozměr času a je stěžejní v úvahách o teplotní setrvačnosti konstrukce. Vypočítá se přímo z parametrů jednovrstvé konstrukce podle vztahu

kde C (J·m^-2K^-1) je tepelná kapacita vztažená na jednotku plochy zdiva a k (Wm^-2K^-1) je součinitel tepelného prostupu (nezaměňovat se součinitelem prostupu tepla U o stejném fyzikálním rozměru). Vyjádříme-li vztah (2) pomocí známých materiálových konstant - měrného tepla c, objemové hmotnosti ρ a součinitele tepelné vodivosti λ, dostáváme

kde D je tloušťka vrstvy a a = λ/(ρ.c) (m²/s) je součinitel teplotní vodivosti (nezaměňovat se součinitelem tepelné vodivosti λ). Součinitel teplotní vodivosti a je materiálovou konstantou, která má zásadní fyzikální význam v úvahách o teplotní setrvačnosti a vystupuje jako klíčový parametr v diferenciální rovnici vedení tepla, např. [2].

Co je relaxační doba ve stavitelství

Relaxační doba je vlastnost obálky budovy, která vyjadřuje její vliv na setrvačnost interiérové teploty po přerušení vytápění či klimatizace. Vliv vnitřních konstrukci (podlahy, stropy, stěny) tato veličina nezahrnuje, může tak ale učinit projekt.

Známe-li relaxační dobu obálky budovy τ_BUD, snadno odhadneme průběh jejího chladnutí od přerušení dodávky tepla při stálé venkovní teplotě:

Znovu dodejme, že teplo akumulované vnitřními konstrukcemi, které zpomaluje chladnutí interiéru, nezapočítáváme.

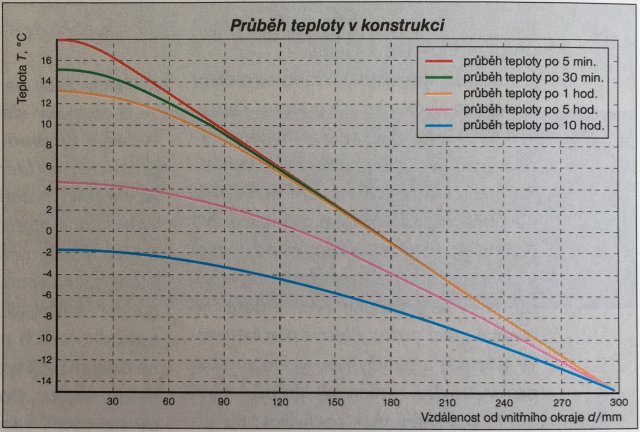
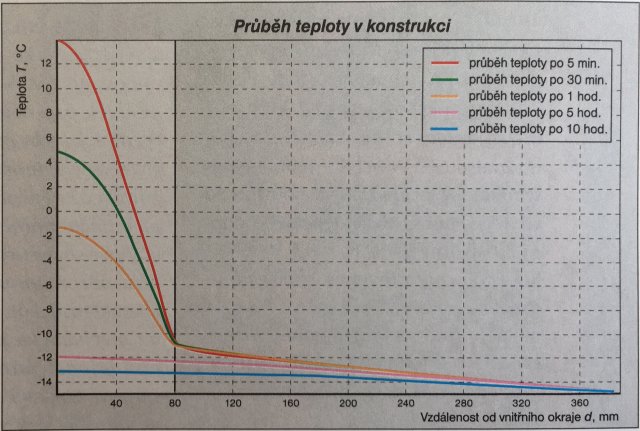
Z rovnice (3) je pak na první pohled zřejmý jednoduchý reciproční vztah mezi součinitelem teplotní vodivosti a a relaxační dobou τ₀ v případě jednovrstvého zdiva. Relaxační doba zde navíc zahrnuje i geometrický člen - čtverec tloušťky zdiva- takže jde o parametr zdiva, nikoli jen o materiálovou konstantu. V reálné skutečnosti ovšem ochlazování neprobíhá za stacionárních podmínek - vrstvy bližší vnitřnímu povrchu chladnou v našem modelu vypnutého vytápění rychleji, viz obr. 2 a 3. Ukážeme ale, že relaxační doba je velmi užitečná veličina pro rychlý, přesto ale věrohodný odhad teplotní setrvačnosti obvodové konstrukce.

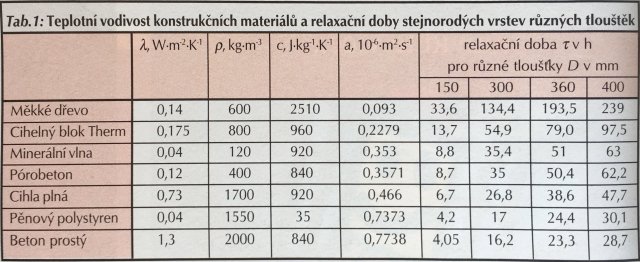
V tab. 1 jsou uvedeny mj. hodnoty tepelné i teplotní vodivosti, měrného tepla a relaxační doby konstrukčních vrstev různých tlouštěk pro některé materiály. Mezi různými materiály je na první pohled patrné výjimečné postavení dřeva. Dřevo velmi málo vede teplo (nízký součinitel tepelné vodivosti λ) a hodně jej akumuluje (vysoké měrné teplo). Takto extrémně výhodná kombinace (z hlediska teplotní setrvačnosti), která u dřeva vede k velmi nízké hodnotě teplotní vodivosti a vysokým relaxačním dobám, je mezi nejznámějšími konstrukčními materiály naprosto výjimečná. Velmi dobré hodnoty teplotní vodivosti vykazuje i cihelný termoblok, ačkoliv klasická cihla je na tom spíše hůře.

Materiály s akumulací tepla, nástroj proti teplotním šokům

Budovy mohou být stavěny z rozmanitých materiálů. Dle jejich hmotnosti dělíme výsledné objekty na lehké (malá akumulace tepla) a stavby těžké (s výbornou teplotní setrvačností). A…

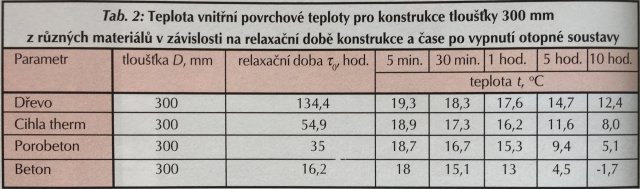
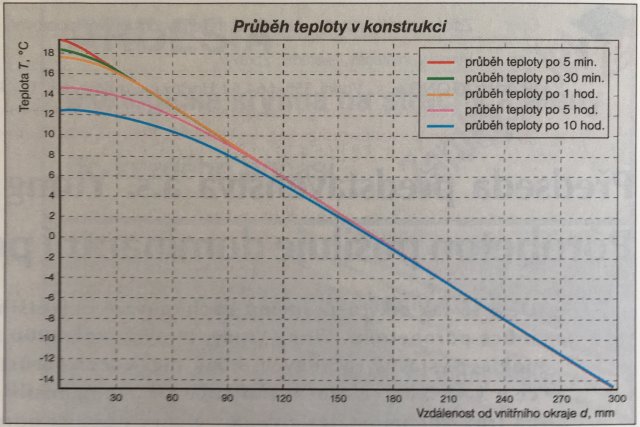
Podstatná je však otázka, jak se projeví relaxační doba na rychlosti chladnutí vnitřního povrchu obvodové konstrukce. Předpokládejme, že ve stavu ustáleného tepelného proudění konstrukcí je vnitřní povrchová teplota 20 ˚C a vnější –15 ˚C. Odpojení otopné soustavy budiž simulováno podmínkou nulového tepelného toku na vnitřním okraji konstrukce (= první okrajová podmínka). Vnější (venkovní) okraj budiž udržován na konstantní teplotě –15 ˚C (= druhá okrajová podmínka). Průběh poklesu teploty v závislosti na čase a vzdálenosti od okrajů byl počítán s použitím rovnice vedení tepla s uvedenými okrajovými podmínkami metodou sítí, např. [3]. Výpočtový program byl vypracován ve středisku Multimédia vydavatelství Vega v prostředí Delphi. Na obr. 1 a 2. je grafický výstup tohoto výpočtu pro dřevo a beton. Výsledky poklesu povrchových teplot na vnitřní straně konstrukce (jednovrstvé, stejnorodé) ukazuje tab. 2.

Z tab. 2 je vidět, že pokles teploty - tj. chladnutí - po odpojení otopné soustavy je větší pro konstrukce s menší relaxační dobou. Tento pokles je u konstrukcí s velmi nízkou relaxační dobou po delších časech chladnutí výrazný, viz srovnání dřevo - beton po 10 hodinách. Aby naopak betonová zeď chladla na vnitřním povrchu stejně rychle jako dřevo tloušťky 300 mm, musela by mít tloušťku 865 mm, jak plyne z krátkého výpočtu.

Vícevrstvé konstrukce

Pokud jde o stanovení relaxační doby vícevrstvé sestavy, postupuje se stejně, jako v případě jediné vrstvy. Spočítá se teplo, které se uvolní »stacionárním« ochlazením jednotkové plochy konstrukce o malou hodnotu dt a toto teplo se postaví rovno počátečnímu tepelnému toku procházejícímu venkovním povrchem po dobu τ. Relaxační doba τ₀, což je více či méně komplikovaná funkce tloušťky, tepelné a teplotní vodivosti jednotlivých vrstev, se určí opět jako konstanta nepřímé úměrnosti ze vztahu (1). Pro relaxační dobu τ₀(n) konstrukce o n vrstvách (počítaných z venkovní strany; venkovní vrstva má index i=1) platí

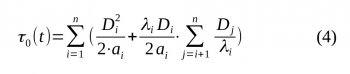
kde D_i je tloušťka, λ_i - tepelná vodivost a a_i - teplotní vodivost i-té vrstvy. Pro n = 1 (jedna vrstva) dostaneme výraz (1); pro n = 2 dostaneme

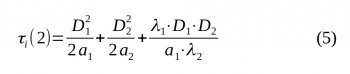
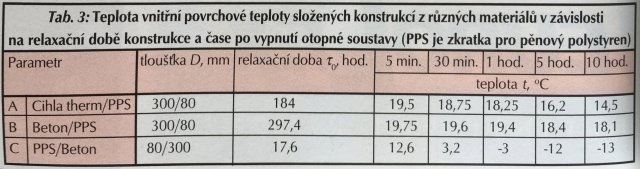
V případě konstrukce složené z několika fyzikálně odlišných vrstev nás opět zajímá chladnutí vnitřního povrchu s časem po vypnutí otopné soustavy. Z (4) i (5) je vidět, že hodnota relaxační doby pro vícevrstvé konstrukce závisí na pořadí vrstev, což je logické. Např. betonová konstrukce chladne pomaleji, je-li izolována polystyrenem zevnitř, než když je izolována zvnějšku. Obecně vícevrstvá konstrukce bude chladnout tím pomaleji, čím menší bude tepelný tok vnějším povrchem ze zdiva ven; přitom je ale podstatné vědět, na jaké teplotě se vlastně nachází vrstva s dominující tepelnou kapacitou. Zajímavé příklady, které stručně okomentujeme, ukazuje tab. 3.

(A) Zateplíme-li z vnější strany cihelný blok typu therm deskou polystyrenu 80 mm, docílíme podle očekávání vyšší relaxační doby, neboť polystyren brání úniku tepla akumulovaného cihlami do okolí. Rychlost chladnutí vnitřního povrchu konstrukce při vypnutém vytápění bude znatelně menší než u neizolovaného zdiva - 5,5 ˚C oproti 12 ˚C za 10 hodin - srov. tab. 2.

Příklad konstrukce s akumulací tepla

Jestliže chceme v našich domech nejen šetřit za vytápění a chlazení, ale i žít v celoročně příjemném prostředí se stabilní teplotou, potom si jen s tepelnou izolací, ať je jakkoli…

(B) Opatříme-li betonovou konstrukci, která podle tab. 2 patří mezi nejhorší z pohledu teplotní setrvačnosti, získáme doslova skvost! Relaxační doba je téměř 300 hodin a vnitřní teplota konstrukce v našem modelu po 10 hodinách vypnuté otopné soustavy nespadne ani na 18 ˚C (oproti -1,7 ˚C u betonové zdi bez izolace, viz. tab. 2). Příčinou je polystyren, který brání úniku velkého množství v betonu akumulovaného tepla. Podobně se chová sestava plná cihla (300 mm) - izolace (80 mm).

(C) Zaizolujeme-li beton polystyrenem zevnitř, docílíme opaku. Beton je udržován na nízké teplotě, která se po vypnutí vytápění ještě rychle snižuje. Na vnitřním povrchu konstrukce se již za pouhou hodinu objeví teplota –3 ˚C, viz obr. 3. Snadné přizpůsobení polystyrenu teplotě chladného jádra po odpojení vytápění, které je dáno především jeho velmi nízkou objemovou hmotností a tedy velmi nízkým měrným teplem vztaženým na jednotku objemu, může být příčinou tepelné nepohody.

Unikum zvané mastek

Mastek, občas nazývaný jako talek, hrnčířský kámen nebo třeba lojovec, je minerál, který si zaslouží alespoň část pozornosti nás, kteří dáváme přednost přírodním materiálům. Jeho…

Literatura a zdroje:

[1] Hejhálek Jiří: Zdicí materiály, úspory za vytápení, životnost a tepelná pohoda. Stavebnictví a interiér 12/2000, str. 46. Hradec Králové, VEGA 2000.
[2] Horák Zdeněk, krupka František: Fyzika, příručka pro vysoké školy technického směru, str. 332. Praha, SNTL 1976.
[3] Rychnovský Richard, Výborná Jarmila: Parciální diferenciální rovnice a jejich některá řešení, str. 141. Praha, SNTL - Polytechnická knižnice II. sv. 28